Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan.
The exterior derivative d has the property that d2 = 0 and is the differential (coboundary) used to define de Rham cohomology on forms. Integration of forms gives a natural homomorphism from the de Rham cohomology to the singular cohomology of a smooth manifold. The theorem of de Rham shows that this map is actually an isomorphism. In this sense, the exterior derivative is the "dual" of the boundary map on singular simplices.
Contents |
Definition
The exterior derivative of a differential form of degree k is a differential form of degree k + 1. There are a variety of equivalent definitions of the exterior derivative.
Exterior derivative of a function
If ƒ is a smooth function, then the exterior derivative of ƒ is the differential of ƒ. That is, dƒ is the unique one-form such that for every smooth vector field X, dƒ(X) = Xƒ, where Xƒ is the directional derivative of ƒ in the direction of X. Thus the exterior derivative of a function (or 0-form) is a one-form.
Exterior derivative of a k-form
The exterior derivative is defined to be the unique R-linear mapping from k-forms to (k+1)-forms satisfying the following properties:
- dƒ is the differential of ƒ for smooth functions ƒ.
- d(dƒ) = 0 for any smooth function ƒ.
- d(α∧β) = dα∧β + (−1)p(α∧dβ) where α is a p-form. That is to say, d is an antiderivation of degree 1 on the exterior algebra of differential forms.
The second defining property holds in more generality: in fact, d(dα) = 0 for any k-form α. This is part of the Poincaré lemma. The third defining property implies as a special case that if ƒ is a function and α a k-form, then d(ƒα) = dƒ∧α + ƒ∧dα because functions are forms of degree 0.
Exterior derivative in local coordinates
Alternatively, one can work entirely in a local coordinate system (x1,...,xn). First, the coordinate differentials dx1,...,dxn form a basic set of one-forms within the coordinate chart. Given a multi-index I = (i1,...,ik) with 1 ≤ ip ≤ n for 1 ≤ p ≤ k, the exterior derivative of a k-form
over Rn is defined as
For general k-forms ω = ΣI fI dxI (where the components of the multi-index I run over all the values in {1, ..., n}), the definition of the exterior derivative is extended linearly. Note that whenever i is one of the components of the multi-index I then dxi∧dxI = 0 (see wedge product).
The definition of the exterior derivative in local coordinates follows from the preceding definition. Indeed, if ω = ƒI dxi1∧...∧dxik, then
Here, we have here interpreted ƒI as a zero-form, and then applied the properties of the exterior derivative.
Invariant formula
Alternatively, an explicit formula can be given for the exterior derivative of a k-form ω, when paired with k+1 arbitrary smooth vector fields V0,V1, ..., Vk:
where ![[V_i,V_j]](/2012-wikipedia_en_all_nopic_01_2012/I/1af903dda57a004d32d5f5234d61a539.png) denotes Lie bracket and the hat denotes the omission of that element:
denotes Lie bracket and the hat denotes the omission of that element:
In particular, for 1-forms we have: dω(X,Y) = Xω(Y) − Yω(X) − ω([X,Y]), where X and Y are vector fields.
Examples
- 1
Consider σ = u dx1∧dx2 over a 1-form basis dx1,...,dxn. The exterior derivative is:
The last formula follows easily from the properties of the wedge product. Namely,  .
.
- 2
For a 1-form σ = u dx + v dy defined over R2. We have, by applying the above formula to each term (consider x1 = x and x2 = y) the following sum,
Further properties
Closed and exact forms
Differential forms in the kernel of d are called closed forms. The image of d are called exact forms. Closed and exact forms are related, because of the identity d(dα) = 0 for any k-form α. This implies that every exact form is closed. The converse is true in contractible regions, by the converse to the Poincaré lemma.
Naturality
The exterior derivative is natural. If ƒ: M → N is a smooth map and Ωk is the contravariant smooth functor that assigns to each manifold the space of k-forms on the manifold, then the following diagram commutes
so d(ƒ*ω) = ƒ*dω, where ƒ* denotes the pullback of ƒ. This follows from that ƒ*ω(·), by definition, is ω(ƒ*(·)), ƒ* being the pushforward of ƒ. Thus d is a natural transformation from Ωk to Ωk+1.
The exterior derivative in calculus
Most vector calculus operators are special cases of, or have close relationships to, the notion of exterior differentiation.
Gradient
A smooth function f: Rn → R is a 0-form. The exterior derivative of this 0-form is the 1-form
That is, the form dƒ acts on any vector field V by outputting, at each point, the scalar product of V with the gradient ∇ƒ of ƒ.
The 1-form dƒ is a section of the cotangent bundle, that gives a local linear approximation to ƒ in the cotangent space at each point.
Divergence
A vector field V = (v1, v2, ... vn) on Rn has a corresponding (n-1)-form
where 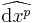 denotes the omission of that element.
denotes the omission of that element.
(For instance, when n = 3, in three-dimensional space, the 2-form ωV is locally the scalar triple product with V.) The integral of ωV over a hypersurface is the flux of V over that hypersurface.
The exterior derivative of this (n−1)-form is the n-form
Curl
A vector field V on Rn also has a corresponding 1-form
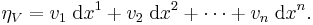 ,
,
Locally, ηV is the dot product with V. The integral of ηV along a path is the work done against -V along that path.
When n = 3, in three-dimensional space, the exterior derivative of the 1-form ηV is the 2-form
Invariant formulations of grad, curl, div, and Laplacian
The three operators above can be written in coordinate-free notation as follows:
where  is the Hodge star operator and
is the Hodge star operator and  and
and  are the musical isomorphisms.
are the musical isomorphisms.
See also
- Exterior covariant derivative
- de Rham complex
- Discrete exterior calculus
- Green's theorem
- Lie derivative
- Stokes' theorem
References
- Flanders, Harley (1989). Differential forms with applications to the physical sciences. New York: Dover Publications. pp. 20. ISBN 0-486-66169-5.
- Ramanan, S. (2005). Global calculus. Providence, Rhode Island: American Mathematical Society. pp. 54. ISBN 0-8218-3702-8.
- Conlon, Lawrence (2001). Differentiable manifolds. Basel, Switzerland: Birkhäuser. pp. 239. ISBN 0-8176-4134-3.
- Darling, R. W. R. (1994). Differential forms and connections. Cambridge, UK: Cambridge University Press. pp. 35. ISBN 0-521-46800-0.



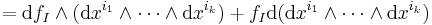
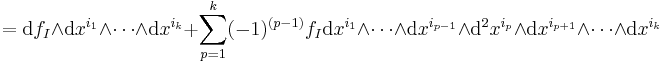
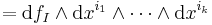
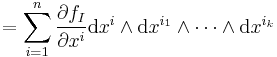

![%2B\sum_{i<j}(-1)^{i%2Bj}\omega([V_i, V_j], V_0, \ldots, \hat V_i, \ldots, \hat V_j, \ldots, V_k)](/2012-wikipedia_en_all_nopic_01_2012/I/64a21f413a45ec9d68ad42081d1323b6.png)
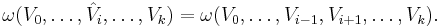



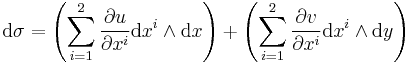


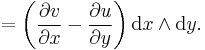
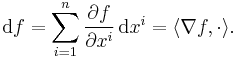


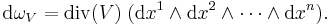

![\begin{array}{rcccl}
\operatorname{grad}(f) &=& \nabla f &=& \left( {\mathbf d} f \right)^\sharp \\
\operatorname{div}(F) &=& \nabla \cdot F &=& \star {\mathbf d} \left( \star F^\flat \right) \\
\operatorname{curl}(F) &=& \nabla \times F &=& \left[ \star \left( {\mathbf d} F^\flat \right) \right]^\sharp, \\
\Delta f &=& \nabla^2 f &=& \star {\mathbf d} \left( \star {\mathbf d} f \right) \\
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/d3b071acf817e21664511670cf1be3d0.png)